Geogebra Explorations
In this portion of the task you will use the free downloadable software, Geogebra to create sketches that verify discoveries found by Ptolemy and Menelaus and to prove the sum and difference formulas for sine and cosine. All of your sketches must be constructed so that when points are dragged lines remain parallel or perpendicular as required. On the Geogebra Tutorial page you can find an online manual for using Geogebra, video tutorials, links to explanations with screenshots, and a PDF manual that you can download.
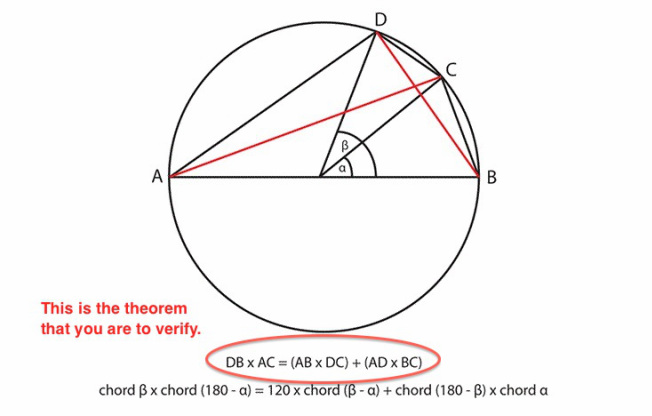
Exploration #1 Ptolemy's Theorem
Create the sketch below in Geogebra, labelled exactly as it is here. Points A and B must form the diameter, AB of the circle so be certain the segment passes through the center, through construction. Points C and D should be dynamic - you should be able to grab and drag them. Insert measurements and a calculation which demonstrates that Ptolemy's Theorem is always true. This does not constitute a proof of the theorem. For that, click on the above title to go to Cut the Knot for several versions of proof.
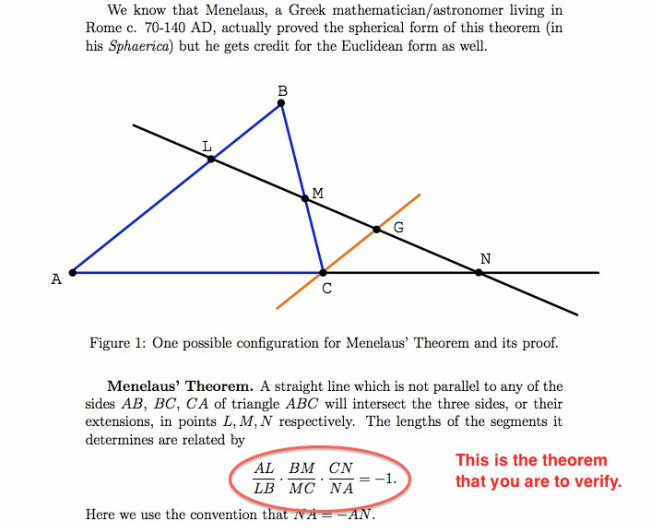
Exploration #2 Menelaus' Theorem
In Geogebra create a construction of the diagram below. The segment CG should be constructed so that it is parallel to segment AB. All of the vertices of triangle ABC should be dynamic. Verify that Menelaus' Theorem holds true as you move the vertices by showing measures of lengths and the calculation of the product of ratios in the theorem.
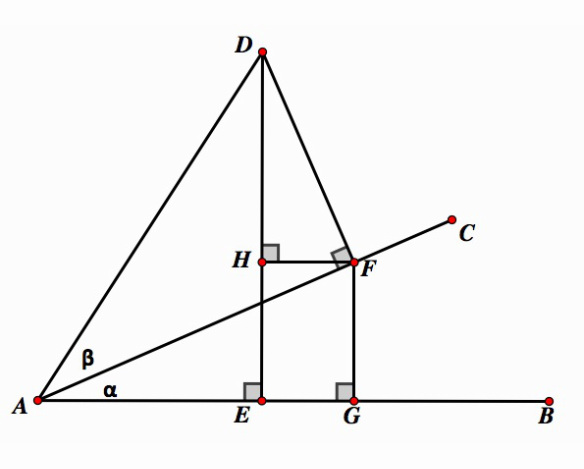
Exploration #3
Geometric Proof of the Sum and Difference Identities
Construct the sketch shown below in Geogebra. Angles that are indicated as right angles must be constructed so that they remain right as other points are dragged. Use this construction to formally prove the sum and difference identities for the sine and the cosine. This proof while require using similar triangles.